Observations: Fundamentals of Investment Valuation

Tuesday, August 24, 2010

Fundamentals of Investment Valuation

As we saw in Bond Basics, a bond typically represents an obligation by the borrower to pay fixed amounts of interest on fixed dates, and to repay the principal amount when the bond matures. The relative certainty of the amounts and dates is the major advantage of bonds compared to other possible investments. Bond valuation, then, is assigning a value or price to this stream of payments.

Intro to Present Value: What is $105 a Year from Now Worth to You Now?

The key to pricing bonds is the concept of Present Value, or PV. Suppose you can earn 5% interest and you have $100. From the bond basics post we know that interest = principal x rate x time. So, in one year $100 will earn ($100 x 5% x 1 =) $5 in interest.

Therefore, a year from now you can have $105 -- your original $100, plus $5 in interest. It is in that sense that the "present value" of $105 a year from now is said to be $100; $105 a year from now is worth $100 today. Note that the $105 total at the end is equal to the $100 initial investment times (1 + the interest rate), or $100 x (1 + 5%), or $100 x 1.05.

It follows that $100 would be worth $105 x 1.05 = $110.25 two years from now. Or, equivalently, the present value of $110.25 two years from now is $100 (assuming a 5% interest rate).

Note: For this analysis, I am ignoring the impact of taxes and any transaction costs.

Simple Bond Pricing Example

Bond Pricing Example

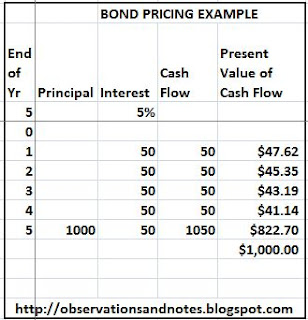
The table above (click to enlarge) shows the expected cash flow from a hypothetical 5-year risk-free bond. The bond pays $50 in interest at the end of each year, and the $1000 principal is returned at the end of the 5 years. I have combined those cash flows in the column labeled "Cash Flow."

The "Present Value of Cash Flow" column shows the present value of each year's payment, assuming a 5% interest rate. Since $47.62 x 1.05 = $50, the present value of $50 a year from now is $47.62. The present value of $50 two years from now is $45.35, etc.

If you add all of the present values together, you get the present value of all of the expected receipts -- $1,000. If all of the future expected receipts are worth $1,000 now, it makes sense that a buyer would be willing to pay $1,000 for this bond. That's not surprising since this is, in fact, a $1,000 bond. (Note: to see the Excel spreadsheet with the actual formulas, click here.)

Present Value is the Key to Investment Analysis

The concept of present value is arguably the key concept in investment analysis. Every investment can be viewed as a stream of future cash flows. The critical question for an investor is how much is the investment worth? The present value methodology can help the investor answer that question whether he is buying bonds, stocks, or rental properties -- or even building a new chemical plant. I've introduced the concept here because I think it's easiest to understand in the context of simple bonds. However, the approach is equally applicable to other types of investments.

The next post in this series discusses yield to maturity and interest rate risk.

For a practical example of the application of these concepts in retirement planning, see my Retirement Model.
For a list of other popular posts, see the sidebar to the left or the menu bar at the top of the page.